Michael's Website

후배중에 요즘 Discreet Combustion을 이용한 영상 작업을 하는 친구가 있는데, 작년에 Combustion 책을 썼었다. 그 당시 나에게 부탁을 해서 Combustion Script에 대한 글을 부탁해서 써줬는데 여기에서 소개할까한다.

컴버스쳔 스크립트를 이용한 파티클
컴퓨터를 사용하는 대부분의 경우 수학을 조그만 응용하면 멋진 결과를 얻을 때가 많습니다. 컴버스쳔처럼 수학 함수를 사용할 수 있는 스크립트를 제공하는 프로그램의 경우, 약간의 수학적 지식을 동원하면 일일이 손으로 키를 잡지 않더라도 멋진 효과를 만들어 낼 수 있죠.

지금부터 수학적으로 잘 알려진 50개의 곡선 중 멋진 효과를 보여주는 3가지 곡선, 애스트로이드(Astroid), 에피시클로이드(Epicycloid), 히포시클로이드(Hypocycloid)를 소개하고, 이 곡선을 컴버스쳔의 스크립트로 적용하는 법을 알아보도록 하겠습니다.

애스트로이드(Astroid)

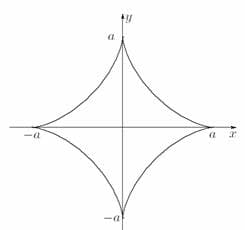
애스트로이드는 4개의 원의 호로 연결되어 있는 형태의 곡선으로 곡선의 방정식은 다음과 같습니다.
어떠한 좌표계를 쓰느냐에 따라서 수식이 조금씩 달라질 수 있는데 좌표계에 따른 이 곡선의 표현식은 다음과 같습니다.

데카르트 방정식

매개변수 방정식

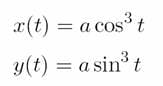
여러 방정식 중에서 컴퓨터 프로그램으로 전환하기 좋은 방정식은 주로 매개변수 방정식입니다. 매개변수 방정식은 변수값 t가 변함에 따라서 해당하는 X(t)값과 y(t)값이 나오기 때문에 바로 프로그램으로 적용할 수 있습니다.

위의 공식을 컴버스쳔에 적용시키면 채널에 따라서 다음의 수식을 입력함으로써 위의 모양으로 움직이는 곡선을 만들 수 있습니다.

X채널

// Author : Kang, Hyungjun
XCenter = 320.0
Frequency = 0.3
a = 100

t = (CB.GetCurrentFrame() * Frequency * Math.PI) / 180
// Astroid
a * Math.cos(t) * Math.cos(t) * Math.cos(t) + XCenter

Y채널

// Author : Kang, Hyungjun
YCenter = 240.00;
Frequency = 0.30;
a = 100;
t = CB.GetCurrentFrame() * Frequency * Math.PI / 180;
// Astroid
a * Math.sin(t) * Math.sin(t) * Math.sin(t) + YCenter;

CB.GetCurrentFrame()를 통해서 현재 프레임수를 받아오게 되면 이것을 레디안 값으로 바꿔주기 위해서 180 / Math.PI를 곱해줍니다. Math.PI는 3.141592로 나가는 값입니다.

매개변수인 t가 정해졌으니 이제 각 채널별 결과값은 위의 공식대로 값을 입력한 결과이죠. 화면 한 가운데서 곡선이 움직이게 하기 위해서 화면크기의 절반인 320과 240을 곱해줬습니다. 이 결과 나타나는 화면의 곡선은 다음과 같습니다.